Problematika rizikově očištěného výnosu

I když se mnohdy můžeme setkat s otázkou investorů kolik daná investice vydělala, je nutné brát v potaz nejen absolutní výnos, ale podívat se také na riziko s tímto související a dále zkombinovat tyto dvě veličiny a vyjádřit je finálním poměrem, který by nám měl definovat tzv. rizikově očištěný výnos. Takovou modlou v průmyslu je Sharpeho poměr. Tento poměr byl vyvinut v r. 1966 laurátem Nobelovy ceny Williamem Sharpem (původně nazváno jako poměr výnosu a volatility) je dnes v podstatě standard v investičním průmyslu pro měření rizikově očišťeného výnosu. Měří dodatečný průměrný výnos po odečtení roční bezrizikové ůrokové sazby v čitateli a volatilitou vyjádřenou směrodatnou odchylkou (volatilitou měsíčních výnosů dané investice) vyjádřenou na roční bázi. Tudíž můžeme psát následující:
Sharpeho poměr = (průměrný roční výnos – roční bezriziková úroková sazba)/roční směrodatná odchylka
To znamená, cílem je mít stejný nebo lepší výnos po odečení bezrizikové sazby na trhu na jednotku podstupovaného rizika, v tomto případě volatility investice. Ono, daná bezriziková sazba představuje v praxi při výpočtech Sharpeho poměru jistou komplikaci a to ve smyslu hodnocení investicí za použití jiné tzv. finanční páky. Tj. dejme tomu, že se manažer rozhodne pro to, že pro daný program by mělo stačit jako požadovaný počáteční kapitál polovina vkladu oproti současnému stavu. Pro lepší demonstraci dané problematiky pak předpokládejme, že bezriziková sazba na trhu činí 3% (při vyšší sazbě toto více vynikne). Za použití dvojnásobné páky manažerem programu pak pochopitelně dojde také ke zdvojnásobení dosaženého průměrného ročního výnosu a zdvojnásobení rizika vyjádřeného roční směrodatnou odchylkou výnosů (samozřejmě hypoteticky a za předpokladu nezměněné situace ve výkonnosti, či při rekalkulaci výsledku zpětně). Jak se tedy změní Sharpeho poměr po zdvojnásobení finační páky alias snížení požadovaného kapitálu na polovinu? V příkladě použijme vykonstruované údaje výnosů a rizika pro názornost:
Současný stav Sharpeho poměr = (15% výnos – 3% bezriziková sazba)/ 10% volatilita výnosů = 1,2
Budoucí stav Sharpeho poměr = (30% – 3% bezriziková sazba)/ 20% volatilita výnosů = 1,35
Takže na příkladu vidíme, že v podstatě program jako takový se nezměnil, jen se změnila finanční páka při použití o poloviny nižšího vkladu. Poměr výnos/ riziko by však měl zůstat zachován (oba dva jak čitatel, tak jmenovatel se zdvojnásobily), Avšak daná bezriziková sazba způsobila v poměru změny a vlastně více pákovou investici podle Sharpeho poměru zvýhodnila. Tento by měl být zachován a proto se v praxi často pak používá modifikovaná forma Sharpeho poměru vyjádřena bez této bezrizikové sazby:
Modifikovaný Sharpeho poměr = průměrný roční výnos/ roční směrodatná odchylka výnosů
Zde pak již po změně finanční páky nedojde ke změně Sharpeho poměru, za jinak stejných okolností.
Sharpeho poměr se neobejde bez určitých nedostatků, které je potom nutné eliminovat za použití jiných ukazatelů rizikově očišťeného výnosu a následně pak poměry brát jako komplex při vyhodnoceních investic s ohledem na rizikové preference investora. Jaké tedy jsou nedostatky ukazatele Sharpeho poměru? Jednak se jedná o to, že ač ukazatel volatility (směrodatné odchylky) ve jmenovatli poměru je důležitý ukazatel rizika, má své dvě stránky a to volatilitu tu nežádoucí při vyšších negativních výnosech, tak také pozitivní stránku ve formě vyšších pozitivních výnosů. Sharpeho poměr tak v podstatě bere ja větší negativní výnosy, tak větší pozitivní výnosy jako stejně špatnou věc. Manažer, který pak dosáhl daného zhodnocení při občasných větších výnosech v kombinaci s malými výnosy na tom podle Sharpeho poměru může být stejně jako ten manažer, který měl kombinaci průměrných propadů s trochu nadprůměrnými výnosy a nakonec došli ke stejnému cíli tak říkajíc. Přitom mají stený průměrný roční výnos i volatilitu těchto výnosů ve sledovaném období.
Dalším úskalím při použití Sharpeho poměru je to, že nerozlišuje rozdělení ziskových a ztrátových období a výsledkem je podobný či identický Sharpeho poměr, i když ve sledovaném časovém horizontu došlo k sérii táhnoucích se propadů následovaných sérií zhodnocení oproti rovnoměrnějšímu rozložení pozitivních a negativních období. Volatilita těchto propadů se však nevzdalovala moc od průměru, stejně jako u rovnoměrného rozložení výnosů, tudíž jmenovatel Sharpeho poměru zůstává nezměněn. Nejlépe je pak toto demonstrovat graficky následovně (pro zvětšení klikněte na obrázek):
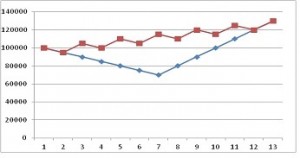 Hypotetická prezentace, zdroj: Lembros Commodity Advisors LLC
Hypotetická prezentace, zdroj: Lembros Commodity Advisors LLC
Na obrázku oba dva programy zhodnotily stejně 30 tis. USD za sledované období při stejném Sharpeho poměru. Co je viditelné je však to, že jeden program zaznamenal relativně mnohem větší propad přes 30 tis. USD ve vývoji equity křivky a druhý program byl naopak velmi stabilní ve svých výnosech s malými propady na cestě vzhůru. Při stejném Sharpeho poměru je však zřejmé, že preferován by byl více program se stabilními střídajícími se plus a mínus výnosy v delším období.
I když existuje celá další řada ukazatelů, které se snaží tyto nedostatky Sharpeho poměru napravit jako Sortiniho poměr, Sterlingův poměr, apod., tak i tyto mají své další nedostatky a v podstatě pak v praxi jde, dle mého názoru, nejlépe použít Calmarův ukazatel. Tento poměrový ukazatel rizikově očištěného výnosu byl vyvinut Terry W. Youngem, který publikoval report CMA (California Managed Account Report) a odtud pochází název tohoto poměru CalMaR. Oproti Sterlinogovu poměru, který rovněž využívá při kalkulaci rizika ve jmennovateli pokles v equity, neměří průměrný roční propad v equity křivce programu/ investice, ale celkový maximální propad (drawdown) za 36 měsíců. Ve jmenovateli pak využívá průměrný roční výnos za stejnou periodu 36 měsíců. Tj. zde ve jmenovateli eliminujeme problém „přelévání“ drawdownu z jednoho období do druhého a namísto průměrného ročního propadu měříme max. propad za celé období. Matematicky vyjádříme Calmarův poměr:
Calmarův poměr = (průměrný roční výnos za 36 měsíců)/max. drawdown za 36 měsíců
Tento poměr nám pak říká nejvíce intuitivně, kolik jsme schopni v programu zhodnotit na jednotku rizikového kapitálu. Dle našeho názorů je u poměřování investic jako indexů nebo aktiv, jejichž cena je měřena mnoho let do historie, je dobré odstranit podmínku 36 měsíců a použít „modifikovanou verzi“ Calmarova poměru, kde se zvolí průměrný výnos za delší periodu a taktéž maximální propad (drawdown) za toto období:
Modifikovaný Calmarův poměr = (průměrný roční výnos za stanovené období)/max. drawdown za stejnou periodu
Podle modifikovaného Calmarova poměru je pak výnos akciového indexu S&P 500 z pohledu rizikově očištěného výnosu velmi rizikovou záležitostí. Od roku 1980 totiž růměrný roční výnos činil něco přes 10% avšak propad tohoto akciového indexu činil přes 50%, tj. na jednotku podstupovaného rizika bylo průměrně dosaženo je pětinového výnosu. Jak se při současném vývoji trhu bude vyvíjet riziková složka v Calmarově poměru do budoucna je otázkou a bude zajisté velmi zajímavé sledovat.
Závěrem se pojďme podívat na vývoj populárního kontraktu na S&P 500 akciový index na burze v Chicagu (Globex burzy CME Group, nejbližší kontrakt, měsíční data) zhruba za rok (klikněte na obrázek pro zvětšení):