Korelace a její význam

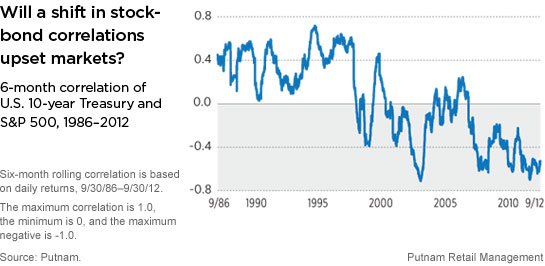
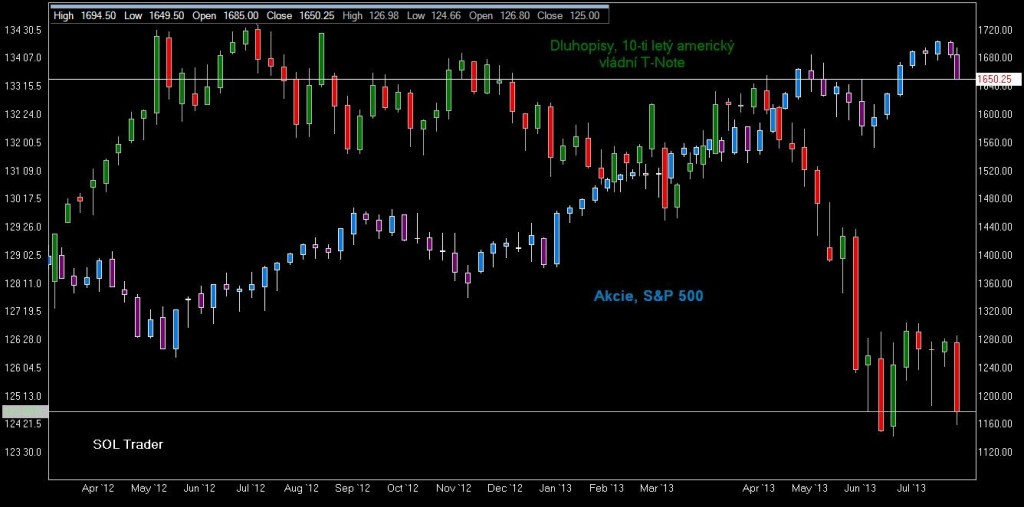
V praxi nezřídka narážím na to, že lidé ne zcela plně rozumí tomu, co znamená v podstatě základ při tvorbě jakéhokoliv portfolia aktiv a to je definice a využití míry korelace. Obvyklá představa zahrnuje např. snahu nakupovat aktiva, která v podstatě místo, aby přispívala svou „nekorelovaností“ mezi sebou tak naopak je výnos jedněch v delším čase negován výnosy druhých. Nebo další představa, že jednotlivé akcie nejsou mezi sebou nekorelovány a je vytvořeno dokonalé portfolio při nějakých 20 různých titulech, apod. (přitom víme, že každá akcie má v podstatě svoji betu, která je mírou závislosti na akciovém trhu jako celku a tudíž jsou již z tohoto titulu tyto aktiva implicitně významně korelovány). V prvním případě se může v poslední době jednat o portfolio akcií a vládních dluhopisů, které bylo populární ještě koncem minulého století (ony formy smíšených fondů), avšak od počátku nového milénia se korelace přibližuje dokonalé negativní a proto v podstatě pokud namixováno v rovnoměrném poměru může znamenat negaci jednoho aktiva druhým. Mimochodem toto je zajímavý fenomén a tak podívejme se na něj graficky:

V druhém případě je to asi nejlépe pak vystižitelné na krizích 2000-2001 technologické bubliny a v současné dluhové a finanční krizi, která eskalovala v r. 2008. Určitě je ješťe v paměťi mnohých pokles indexu Nasdaq 100 od března 2000 do září 2002  kolem 80%! A nebo  akciového indexu S&P 500 od přes 50% od  října 2007 do března 2009! Bohužel s poklesy těchto „diverzifikovaných“ indexů nebyly jediné a další klasická aktiva jako reality a korporátní dluhopisy oslabovaly výrazně na ceně taktéž a ukázaly na výranou korelaci zvláště v období finančního stresu. To zde v USA způsobilo nemalé problémy mnoha lidem a nezřídka některé dostalo do výrazných potíží. A tak pojďmě se na onu statistiku korelace podívat blíže v základní definici a pokusím se oproti klasickým učebnicím vysvětlit co nejjednodušeji a pokud možno nejvíce graficky.

Obcně lze vyjádřit vhodného kandidáta do portfolia např. za pomocí  Sharpeho poměru, který jsme zmínili již minule:

Sharpeho poměr aktiva  > [ Sharpeho poměr portfolia x míra korelace mezi daným aktivem a portfoliem]

To znaméná, aby bylo dané aktivum vhodné do porfolia, tak je nutné aby jeho rizikově očištěný výnos byl vyšší než absolutní hodnota součinu rizikově očištěného výnosu portfolia a míry korelace. A právě ona míra korelace zde hraje klíčovou roli. Pakliže je blízko 0 tak absolutní hodnota součinu bude rovněž bllízko nule a tudíž ono aktivum má velkou šanci být součástí daného portfolia.

Předtím, než popíšeme blíže korelaci jako takovou, tak je nutné zmínit, že tato statistiku je nutné počítat z výnosů, případě logaritmů cenových rozdílů a ne ceny aktiv! Cenová řada trpí tím, co ve statistice nazýváme stacionaritou a výsledná hodnota se může v mnoha příoadech nesprávně lišit od správného výpočtu pomocí výnosů. Na následných grafech však pro lepší intuitivní vizuální představení použijeme cennovou vertikální osu, jak ji obvykle známe.

Co je tedy korelace?

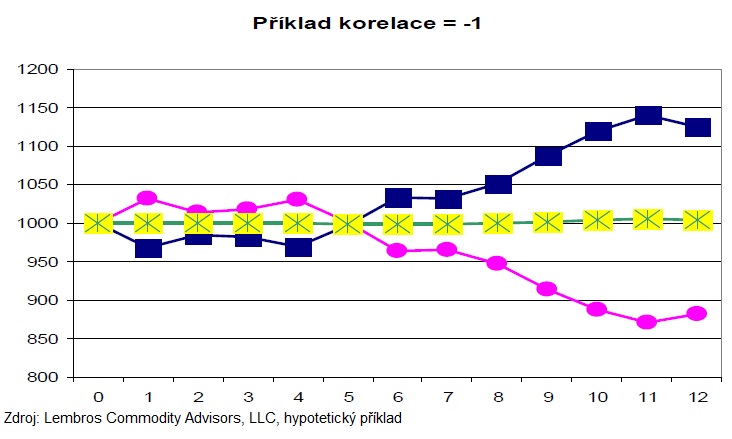
Korelace měří míru závisloti vývoje jedné proměnné na vývoji druhé proměnné (pozor nikoli kauzalitu, tj. že jedna je příčinou druhé!), pohybuje se od -1 naprostá negativní závislost do 1 naprostá pozitivní závislost. Aktiva jsou pak „nekorelovaná“ pokuď je poměr roven 0. Naším cílem je pak nalézt do porfolia takové aktiva, které mají onu korelaci výnosů blízkou nule. Pojďmě se podívat jak vzpadá graficky, když dáme dohromady aktiva s negativní korelací, při zachování stejných vah každého aktiva:

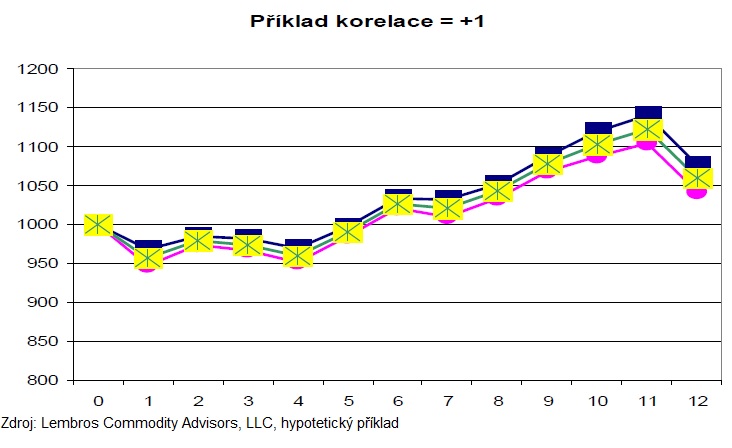
Konečná equity křivka porfolia aktiv vyjádřená na grafu jako ta s hvězdičkama má pak v konečném důsledku průběh vodorovné úsečky. To znamená výnosy z jednoho aktiva mají v čase tendenci eliminovat výnosy aktiva druhého. Nyní, jak vypadá portfolio křivka při kombinaci aktiv s výnosy s korelací +1?:

V tomto příkladě vidíme, že přidání dalšího aktiva do portfolia nepřináší téměř žádnou přidanou hodnotu, jelikož výnosy jsou silně pozitivně korelovány. Navíc, když bude docházek k propadům (viz. onen Nasdaq 100 v r. 2001 nebo S&P 500, reality, atd. v r. 2008-9) pak přidání historicky korelovaných aktiv může jen škody znásobit.

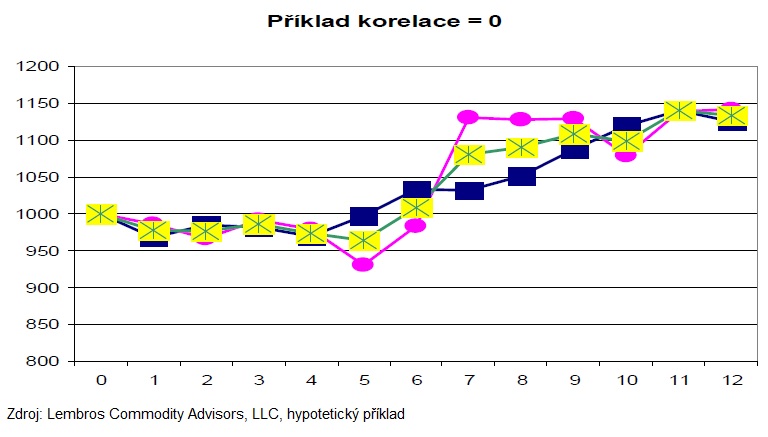
A konečně se pojďme podívat na vývoj equity křivky u relativně nekorelovaných aktiv, resp. aktiv s korelací výnosů blízko nule:

V tomto posledním příkladě je to, o co se snažíme, aby výnosy našich aktiv v portfoliu byla navzájem na sobě nezávislé a tudíž , aby výnosy jednoho aktiva nerušilo výnosy druhého a zároveň, aby v případě propadů cen jednoho aktiva nebyla vysoká pravděpodobnost propadu i druhého. Navíc také, aby další aktivum mělo potenciál v případě propadu jednoho zhodnocovat a redukovat tak volatilitu výnosů celého portfolia a byl dosažen celkově vyšší rizikově očišťený výnos.

Jak matematicky vyjádříme výpočet korelace?

Jednoduše jsme popsali tedy základní kámen stavby každého sofistikovanějšího portfolia a to jest ukazatel miry korelace. V praxi se po proběhlých krizích, které v podstatném měřítku změníly pohled na mnohá aktiva a jejich kombinace v portfoliích, zvláště zde v USA u sofistikovaných investorů (smart money, tj. family offices, apod.) diskutují nutnosti přidávání historicky skutečně nekorelovaných aktiv. Aktiv, které navíc mají tendenci v obdobích značného finančního stresu a zvýšené volatility na trzích (o růstu volatility při poklesech trhů jsme rovněž již psali) na této naopak benefitovat. Ať už se jedná o alternativní investice jako sbírky a ceniny, drahé kovy nebo některé formy hedgeových fondů (managed futures), jež bývají tzv. long volatility, apod.

Závěrem se pojďmě podívat na vývoj cen kontraktů na akciový index (mini S&P) a americké vládní dluhopisy (10-ti leté T-Notes) na burze v Chicagu (Globex system CME Group). Klikněte na obrázek pro zvětšení: