Pomocné metody testování AOS

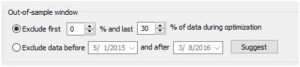
K základnímu testování quant strategií dle backtestu ať už na “viděných in sample” (IS)  nebo “neviděných out of sample”(OOS) datech je možné nebo respektive nutné využít další metody. Jistě je dobré aplikovat vytvořenou strategii na OOS datech a využít například walk-forward metodu, kdy určité procento datové řady je odebráno pro původní vývoj AOS a nádledně  použito v další fázi:

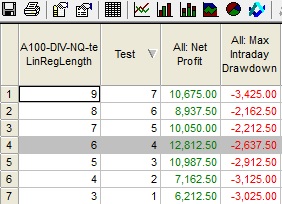
Je nutné si uvěmit, že při vývoji nemáme nekonečné řady a nekonečné množství obchodů a proto vždy bude tendence k takzvanému data snoopingu, to znamená vytváření závěrů zpětným pohledem na data a výsledky backtestu, zvláště pak založeného na násobném kombinování parametrů, a podobně, které nám vytvoří tu nejlepší equity. Proto je nutné zkoumat, zda změny hodnot parametrů neprodukují různé výnosově-rizikové poměry. Metodou je pak test variability parametrů:

Inkrementální změny hodnot parametrů by neměla podstatně menit  výnosově-rizikové poměry  jako čistý zisk nebo průměrný zisk na obchod v poměru k drawdownu.

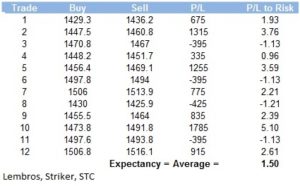
Další metodou je testování principu pozitivního očekávání. To znamená propočet průměrného zisku na obchod v poměru k riziku na obchod.Je důležité, aby jednotlivé vzorky průměrných zisků na obchod u backtestu měly pozitivní poměr. To je pak podstatné zvláště u trendových strategií, kde by měl poměr převyšovat 1, to znamená několikanásobek průměrného zisku na obchod v poměru k riziku na obchod. Příklad propočtu pozitivního očekávání u aplikace AOS na mini MidCap trhu:

V uvedeném příkladě pak je propočtěný průměrný zisk na obchod 1,5-ti násobkem rizika na obchod, čili splňující princip pozitivního očekávání.

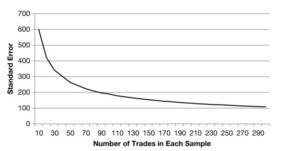
Velice důležité, aby námi vytvářený systém měl na dané datové řadě dostatečný počet obchodů k zachování statistické významnosti. To znamená minimalizovat standardní chybu průměrného zisku na obchod dle zkoumaných vzorků dat. Standardní chyba pak představuje směrodatnou odchylku průměrných zisků na obchod ve vzorcích pro odhad intervalu skutečného průměrného zisku na obchod a je definována jako SO/(n)^1/2 , kde SO je směrodatná odchylka průměrných zisků na obchod a n počet obchodů ve zkoumaném vzorku. Příklad vyjádření vývoje standardní chyby v závislosti na počtu obchodů ve zkoumaných vzorcích dat u vybraného AOS:

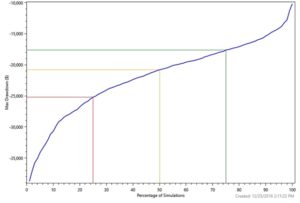
Významnou metodou stress testů je Monte Carlo analýza (MC), vypočítavající pravděpodobnosti dosažení profitů či drawdownů na základě pozměněných posloupností dat z backtestů opakovanými simulacemi. Tímto způsobem se snažíme identifikovat možné extrémnější hodnoty, pro praxi významnějšího charakteru než backtest samotný:

V ukázce se jedná o propočet MC pro jeden z našich komoditních programů na 250 tis. USD počáteční bilanci. Je vidět, že existuje určité jednociferné procento pravděpodobnosti pro dosažení drawdownu převyšující 14%.

Monte Carlo se stalo jistou mantrou, nicméně pozor. Existuje určité úskalí, které je nutno zohlednit při aplikaci simulací. V prní řadě možné porušení autokorelačních charakteristik vývoje obchodů. Je tedy nutné zkoumat, zda existuje pozitivní (zisky následované zisky a ztráty ztrátami v rámci několika zpoždění) či negativní (zisky následované ztrátami a naopak) autokorelace a zda-li je statisticky významná. Dále pak u AOS držící pozici dlouhodobě je nutno zohlednit skutečnost, že pouhé použití zisků/ ztrát zavřených obchodů nebude reflektovat potenciální otevřený profit a dále jeho možnou jeho redukci (open trade equity pullback) na kontinuální bázi.